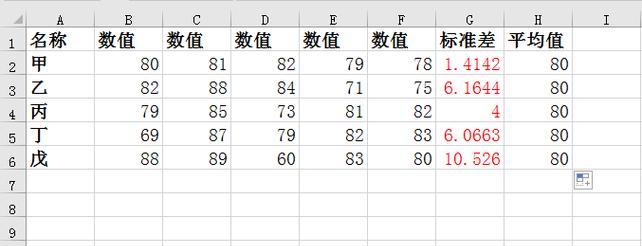
方差是统计学中常用的指标之一,用来衡量数据集的离散程度。在Excel中,我们可以利用内置的方差函数来快速计算数据的方差,并通过公式分析探究方差的含义和应用。本文将介绍Excel中方差计算的公式及其应用场景,帮助读者深入了解方差的计算方法与意义。

了解方差的概念及作用
方差是用来度量数据集中各个数据与其平均值之间的偏离程度的统计量。它能够帮助我们判断数据的离散程度,进而对数据集进行比较、分析和预测。
探索Excel中方差的计算方法
Excel提供了多种方差函数,如VAR.P、VAR.S和VARA等。VAR.P用于计算样本总体方差,VAR.S用于计算样本方差,VARA还可以处理含有逻辑值和文本的数据。我们可以根据具体需求选择合适的函数进行计算。

使用Excel计算样本总体方差
样本总体方差是一种用于描述总体离散程度的统计量。我们可以利用Excel的VAR.P函数来计算样本总体方差,只需输入数据范围即可得到结果。
使用Excel计算样本方差
样本方差是常用的统计量,用于衡量样本数据的离散程度。在Excel中,我们可以利用VAR.S函数来计算样本方差,并通过公式分析深入理解计算过程。
应用场景一:方差在投资组合中的应用
方差在投资组合中被广泛应用,用于评估不同资产的风险程度以及整个投资组合的风险水平。通过Excel的方差计算公式,我们可以快速计算得到投资组合的方差,从而进行风险管理和资产配置。
应用场景二:方差在品质控制中的应用
在品质控制中,方差可以帮助我们评估产品质量的稳定性和一致性。通过Excel的方差计算公式,我们可以对不同批次或不同工序的产品进行方差分析,进而找出影响产品质量的关键因素。
应用场景三:方差在统计推断中的应用
在统计推断中,方差是估计总体方差、检验假设以及构建置信区间等重要步骤中的关键指标。通过Excel的方差计算公式,我们可以进行样本方差的估计、t检验和方差分析等统计推断分析。
注意事项:数据的正确输入和处理
在使用Excel计算方差时,我们需要注意数据的正确输入和处理。确保数据范围的选择准确无误,并排除数据中的异常值和错误值,以避免对方差计算结果产生误导。
进一步分析:方差与其他统计量的关系
方差与其他统计量如标准差、均值等有着密切的关系。通过对方差与其他统计量的计算公式和意义进行对比分析,我们可以更全面地理解数据的特征和离散程度。
案例分析一:股票收益率方差的计算
以股票收益率为例,通过Excel计算股票收益率序列的方差,可以评估股票的风险水平,并为投资决策提供参考依据。
案例分析二:销售额方差的分析
通过Excel计算销售额序列的方差,可以评估销售业绩的波动情况,并进一步分析影响销售额波动的因素,为销售策略的制定提供依据。
案例分析三:学生成绩方差的比较
通过Excel计算不同班级或不同学科学生成绩的方差,可以比较各个班级或学科之间的学生成绩离散程度,从而了解教学质量的差异和改进的方向。
方差计算结果的解读和应用
方差计算结果反映了数据集的离散程度,我们可以通过对方差计算结果的解读和分析,进行决策和预测,优化业务流程和管理策略。
方差计算公式分析的局限性和改进方向
虽然Excel提供了简便的方差计算公式,但在实际应用中仍需注意其局限性。我们可以探索改进方向,如使用更复杂的统计模型或结合其他分析方法来提高预测和决策的准确性。
通过对Excel中方差计算的公式分析,我们可以深入了解方差的计算方法和应用场景,并通过具体案例分析将理论与实践相结合。掌握方差的计算公式及其分析技巧,有助于我们在数据分析和决策中更准确地评估数据的离散程度,提高业务管理和决策的效果。